OP, Opamp, Operationsverstärker: Rauschen bei OPs plus Infos zum Rauschverhalten und der Berechnung eines Low-Noise-Verstärkers

	Verkleinerung der Widerstände
	Rauscharmer Operationsverstärker
	Rauscharmer Operationsverstärker mit Optimierung
	Verringerung der Temperatur
	Weitere Verbesserungsmöglichkeiten

Tips für die Opamp-Auswahl

Verwandte Themen:

	OP in der Praxis
	Operationsverstärkertypen

Allgemeines

Das Rauschen ist etwas, das für viele Leute ein Mysterium ist. Die Entstehung ist zwar tatsächlich einigermaßen komplex, aber die Handhabung der Datenblattwerte eines Operationsverstärkers (gern als OP oder Opamp bzw. OpAmp abgekürzt) ist in der Praxis nicht besonders schwierig, wenn man mit einem Taschenrechner umgehen kann. Auch die Rauschoptimierung der Schaltung auf Basis dieser Werte ist kein Hexenwerk. Nachfolgend ist daher dargestellt, wie man mit den Datenblattwerten umgeht, wie man bezüglich des Rauschens den richtigen Operationsverstärker aussucht, und was man tun muß, damit man die guten technischen Daten nicht durch eine falsche Schaltungsauslegung zunichte macht.

Grundlegendes zum Rauschen

Widerstände rauschen, und das auch in der Theorie; man kann die Rauschspannung sogar berechnen. Dies gilt für jeden ohmschen Widerstand, auch wenn es sich um unerwünschte Übergangswiderstände o.ä. handelt. Die Ursache liegt darin, daß die Elektronen im Material immer in Bewegung sind, wenn die Temperatur höher als der absolute Nullpunkt ist. Durch die völlig zufällige Bewegung geschieht es, daß von einer Momentaufnahme zur nächsten die Elektronen sich im Mittel entweder in Richtung des einen oder anderen Anschlusses bewegen. Wenn sich Elektronen bewegen, ist dies mit einem Stromfluß identisch, und da die Bewegung völlig zufällig erfolgt, ist auch der Stromfluß zufällig, wobei der Mittelwert Null ist. Ein Signal mit zufälligen Werten nennt man Rauschen, weshalb der so erzeugte Strom Rauschstrom genannt wird. Dieser ist sehr klein, kann sich bei einem kleinen Nutzsignal aber durchaus störend bemerkbar machen.

Der Rauschstrom ist abhängig von der Temperatur, denn eine höhere Temperatur bedeutet auch eine höhere Energie der Elektronen im Material, weshalb man von thermischem Rauschen spricht. Man kann es sich so vorstellen, daß die Atome des Widerstands mit steigender Temperatur immer heftiger schwingen (siehe auch

Stromfluß im Leiter) und damit auch die freien Elektronen immer mehr anschubsen. Elektronen, die sich in eine Richtung bewegen, entsprechen dabei einem Stromfluß, wobei man die Spannung bei Kenntnis des Widerstands gemäß dem ohmschen Gesetz berechnen kann. Deswegen ist die Rauschspannung bei einem großen Widerstand auch größer als bei einem kleinen Widerstand. Ein Wissenschaftler namens Boltzmann hatte sich mit dem Rauschen sehr intensiv beschäftigt, weshalb eine wichtige Konstante, mit der man die Rauschspannung berechnen kann, auch seinen Namen trägt: Die Boltzmannkonstante. Das Rauschen besitzt einen Frequenzbereich, der theoretisch unendlich ist. Üblicherweise interessiert das Rauschen aber nur in einem bestimmten Frequenzbereich, beispielsweise bei Audiosignalen bis 20 kHz (Rauschen über 20 kHz hört das Ohr ohnehin nicht). Deswegen berücksichtigt man die begrenzte Bandbreite gleich bei der Berechnung der Rauschspannung. Die Formel hierfür lautet:

Diesem thermischen Rauschen können weitere Effekte überlagert sein, die das effektive Rauschen erhöhen. Diese Effekte, die u.a. bauartbedingt sind, sind übrigens dafür verantwortlich, daß Kohleschichtwiderstände mehr rauschen als Metallschichtwiderstände, die ihrerseits dem theoretischen Ideal ziemlich nahekommen. Mehr Infos über das Rauschen von realen Widerständen finden Sie in

Widerstandsrauschen.

Was in einem "regulären" Widerstand passiert, passiert natürlich auch in einem Halbleiter, der ja auch einen ohmschen Widerstand besitzt. Hinzu kommen noch einige weitere Effekte wie z.B. das Schrotrauschen, das dadurch bedingt ist, daß sich im Betrieb ein Strom durch den Halbleiter bewegt und für einen zusätzlichen stromabhängigen Rauschanteil sorgt. Bei einem Operationsverstärker kann man glücklicherweise alle Effekte in zwei Kenngrößen zusammenfassen, nämlich in Rauschspannung und Rauschstrom. Es handelt sich um rechnerische Werte, die sämtliche Rauschquellen im Operationsverstärker zusammenfassen. Die Rauschspannung addiert sich hierbei zur Signalspannung. Hinzu kommt diejenige Spannung, die durch den Rauschstrom hervorgerufen wird. Dieser bewirkt in den Widerständen der OP-Beschaltung und im Innenwiderstand der Signalquelle eine zusätzliche Rauschspannung. In den Datenblättern von Opamps wird ein Rauschstrom spezifiziert, der aus jedem der beiden Eingänge herausfließt, und eine Rauschspannung, die zwischen den beiden Eingängen anliegt.

Rauschstrom und Rauschspannung beim Opamp

Bild 1: Rauschspannung und Rauschstrom beim Opamp

Die beiden aus dem Plus- und dem Minuseingang herausfließenden Rauschströme fließen bei einem beschalteten Operationsverstärker je durch einen Widerstand nach Masse. Es handelt sich dabei um die Ersatzwiderstände am Plus- und am Minuseingang. Bei bestimmten Schaltungsformen kann auch einer der Widerstände Null sein; beispielsweise beim

invertierenden Verstärker liegt der Pluseingang direkt an Masse. Durch den Rauschstrom wird an diesen Widerständen jeweils eine Rauschspannung hervorgerufen, die man mit dem ohmschen Gesetz als i * R leicht berechnen kann. Jeweils hinzu kommt das thermische Rauschen U_th der beiden Widerstände sowie letztendlich das Spannungsrauschen des Operationsverstärkers.

Bild 2: Rauschbeiträge der Opamp-Beschaltung

Es gibt also insgesamt 5 Rauschbeiträge: Zur Rauschspannung des Opamps kommt die durch den Rauschstrom am Plus-Eingang hervorgerufene Rauschspannung, die durch den Rauschstrom am Minus-Eingang hervorgerufene Rauschspannung, die thermische Rauschspannung der Widerstände am Plus-Eingang und die thermische Rauschspanung der Widerstände am Minus-Eingang hinzu. Diese einzelnen Rauschbeiträge liegen alle an einem der beiden Eingänge an und erscheinen mit der Systemverstärkung des Opamps am Ausgang. Um das Gesamtrauschen zu berechnen, bezieht man sich üblicherweise auf den Eingang und addiert die einzelnen Rauschbeiträge. Glücklicherweise sind diese einzelnen Rauschsignale unkorreliert (=statistisch unabhängig) voneinander, wie man im Fachjargon sagt. Salopp gesagt: Sie rauschen einsam und vor allem unabhängig voneinander vor sich hin. Aus diesem Grund addieren sich die 5 Rauschanteile glücklicherweise nicht linear (also U1+U2+U3+U4+U5) sondern orthogonal sprich als Quadratwurzel aus der Summe der Quadrate, d.h.

. Dies ergibt erfreulicherweise einen kleineren Wert als die lineare Addition.

U1 ist in diesem Fall die Rauschspannung des OPs. Da das Rauschen bandbreitenabhängig ist, wird in den Datenblättern jedoch nicht die Rauschspannung sondern die Rauschspannungsdichte angegeben. Denn der Hersteller kann ja nicht wissen, welche Bandbreite die Schaltung des Anwenders besitzt; Opamps werden ja bei weitem nicht nur in Audioanwendungen eingesetzt. Die angegebene Rauschspannungsdichte muß man lediglich mit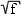

multiplizieren (bei einer Bandbreite von beispielsweise 20.000 Hz also mit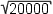

= 141,42) um die Rauschspannung in diesem Frequenzbereich zu erhalten. U2 berechnet sich gemäß dem ohmschem Gesetz durch Multiplikation des Rauschstroms mit dem Wert des externen Widerstand am Plus-Eingang des Opamps, wobei sich Ir wiederum aus der Rauschstromdichte durch Multiplikation mit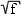

ergibt. Bei U3 gilt das gleiche bezogen auf den Minus-Eingang. U4 ist das Spannungsrauschen der mit dem Pluseingang verbundenen Widerstände und U5 das Spannungsrauschen der mit dem Minuseingang verbundenen Widerstände. Hier eine Übersicht, wie man die einzelnen Rauschanteile berechnet (Zeichenerklärung siehe weiter unten):

Durch Addition der Quadrate und anschließendes Wurzelziehen kann man aus diesen einzelnen Rauschbeiträgen das Gesamtrauschen am Eingang des Operationsverstärkers berechnen:

Durch "Herausziehen" von f kann man die Formel vereinfachen und erhält dann:

Zeichenerklärung:

e_r:		Rauschspannungsdichte
i_r:		Rauschstromdichte
R_P:		Effektiver Widerstand am Pluseingang
R_M:		Effektiver Widerstand am Minuseingang
k:		Boltzmann-Konstante (1,38)
T₀:		Temperatur in Kelvin
f:		Bandbreite in Hz

Das alles hört sich möglicherweise kompliziert an, ist aber im Grunde ganz einfach, wie das Berechnungsbeispiel weiter unten zeigt.

Die Zahlenwerte für Rauschspannung und Rauschstrom kann man den Datenblättern entnehmen, die üblicherweise auf den WebSites der Hersteller frei verfügbar sind. In den Tabellen angegeben sind meistens die Werte bei einer definierten Betriebsspannung, Raumtemperatur und einer Frequenz von 1 kHz. Das Rauschen ist jedoch frequenzabhängig und nimmt bei tiefen Frequenzen hin zu. Aus diesem Grund sind zumindest bei rauscharmen Opamps auch die frequenzabhängigen Kurven in den Datenblättern enthalten. Nachfolgend finden Sie beispielhaft die Rauschkurven eines NE5534A:

Bild 3: Spannungs- und Stromrauschen beim NE5534A

Die Eckfrequenz, unterhalb der das Rauschen zunimmt, ist von Opamp zu Opamp unterschiedlich. Für Audioanwendungen stört ein Anstieg ab ca. 100 Hz kaum, da das menschliche Ohr in diesem Bereich recht unempfindlich auf Rauschen reagiert, während es im Bereich um 2 kHz besonders empfindlich ist. Sollen jedoch Sensorsignale verstärkt werden, ist auch das Rauschen unterhalb von 20 Hz interessant. Für diesen Einsatzzweck kann daher ein Opamp sinnvoll sein, der zwar bei 1 kHz mehr rauscht als ein Konkurrenzmodell, aber eine sehr niedrige untere Eckfrequenz besitzt. Manchmal wird auch die gesamte effektive Rauschspannung im extremen Niederfrequenzbereich (z.B. zwischen 0,1 und 10 Hz) angegeben.

Berechnungsbeispiel

Als Beispiel soll das Rauschen eines Verstärkers mit dem TL071 aus der sehr populären TL07x-Reihe berechnet werden. Die zu berechnende Schaltung ist in Bild 4 dargestellt.

Bild 4: Schaltbild für Rauschuntersuchung

Für das Berechnungsbeispiel sei die Dimensionierung der Schaltung wie folgt:
R1 = 1 MΩ
R2 = 1 MΩ
R3 = 110 kΩ
R4 = 10 kΩ
C1 = 10 μF

Die Signalquelle besitze eine maximale Ausgangsspannung Ug von 10 mV (Effektivwert) und einen Innenwiderstand Rg von 10 kΩ.

Die Rauschspannungunsdichte des TL071 beträgt laut Datenblatt 18 nV/

, die Rauschstromdichte 0,01 pA/

. Diese Werte gelten übrigens selbstverständlich auch für die Typen TL072 und TL074, die 2 bzw. 4 identische OPs in einem Gehäuse beinhalten.

Für die weitere Berechnung muß man das Wechselstrom-Ersatzschaltbild erstellen. Hierin sind kurz gesagt alle Bauteile, die wechselspannungsmäßig eine geringe Impedanz besitzen, wie z.B. Kondensatoren, Spannungsquellen und niederohmige Ausgänge durch Brücken ersetzt. Dann bestimmt man die Impedanz an jedem der beiden Eingänge des Operationsverstärkers. Das Ersatzschaltbild ist in Bild 5 dargestellt.

Bild 5: Ersatzschaltbild für Rauschuntersuchung

Die beiden effektiven Widerstände an den beiden Eingängen des Opamps sind am Pluseingang eine Parallelschaltung aus R1 und Rg sowie am Minuseingang eine Parallelschaltung aus R2 und R3. Die Werte berechnen sich wie folgt:

Mit den oben angegebenen Werten erhält man als Werte R_P = 9,9 kΩ sowie R_M = 99 kΩ. R4 besitzt zwar auch ein thermisches Rauschen, aber es addiert sich lediglich zum Ausgangssignal. Dort erscheinen die anderen Rauschbeiträge um die Systemverstärkung des Opamps verstärkt, sodaß er keine nennenswerte Rolle spielt. Im ersten Schritt wollen wir ihn daher vernachlässigen. Die Schaltung in Bild 3 reduziert sich somit letztendlich zu Bild 6:

Bild 6: Rauschbeiträge der Opamp-Beschaltung

Nun können wir darangehen, die effektive Rauschspannung am Eingang zu berechnen. Wenn man als Bandbreite den Hörbereich, also 20.000 Hz, und als Temperatur 300 K(= ca. 27 °C) annimmt, ergeben sich am Eingang des OPs die folgenden einzelnen Rauschbeiträge:

U1	Spannungsrauschen des Opamps	18 nV/	→	2,55 μV
U2	Stromrauschen am Pluseingang	9,9 kΩ bei 0,01 pA/	→	0,014 μV
U3	Stromrauschen am Minuseingang	99 kΩ bei 0,01 pA/	→	0,14 μV
U4	Therm. Widerstandsrauschen am Pluseingang	9,9 kΩ	→	1,81 μV
U5	Therm. Widerstandsrauschen am Minuseingang	99 kΩ	→	5,73 μV

Zusammengerechnet erhält man eine gesamte Rauschspannung von 6,53 μV am Eingang des Operationsverstärkers. Bemerkenswert ist, daß das vom Operationsverstärker hervorgerufene Rauschen (also das Spannungsrauschen sowie die durch das Stromrauschen am Plus- und Minuseingang verursachten Rauschspannungen) deutlich geringer ist als das thermische Widerstandsrauschen. Bei einer maximalen Ausgangsspannung der Signalquelle von 10 mV ergibt sich gemäß der Formel

ein Signal-/Rauschabstand (also das Verhältnis der Signalspannung zur Rauschspannung) von 63,7 dB. Ob man dabei Signal- und Rauschspannung am Eingang oder am Ausgang miteinander in Relation setzt, ist dabei übrigens völlig unerheblich, denn sowohl Signal- als auch Rauschspannung erscheinen am Ausgang um den Verstärkungsfaktor v verstärkt. Das Verhältnis und damit der Dynamikbereich bleibt dabei gleich.

Da die Signalquelle infolge ihres ohmschen Widerstands selbst rauscht, begrenzt sie selbst den theoretisch möglichen Signal-/Rauschabstand. Bei 10 kΩ beträgt die thermische Rauschspannung bei Raumtemperatur 1,82 μV, was bei 10 mV Signalspannung einen Wert von 74,8 dB ergibt. Dies ist die absolut Grenze; mehr ist bei dieser Signalquelle auch theoretisch nicht machbar.

Wenn Sie sich jetzt fragen, welchen Beitrag der Widerstand R4 zum Gesamtrauschen liefert, können Sie folgende Rechnung anstellen: Sein thermisches Rauschen addiert sich zum bereits berechneten Eingangsrauschen, das um die Systemverstärkung verstärkt aus dem Ausgang heraus kommt. Bei 10 kΩ erhält man bei Raumtemperatur und einer Bandbreite von 20.000 Hz ein thermisches Rauschen von 1,82 μV. Da die Systemverstärkung v=10 beträgt, liegt am Ausgang des Opamps ein Rauschpegel von 65,3 μV an. Addiert man diese Rauschbeiträge wie gehabt orthogonal, ergibt sich ein Gesamtwert von 65,32 μV, d.h. es wirkt sich erst auf die 2. Nachkommastelle aus und ist daher wie eingangs behauptet vernachlässigbar. Alternativ kann man den Rauschbeitrag von R4 durch die Systemverstärkung dividieren und rein rechnerisch dem Eingangsrauschen zuschlagen. Das Ergebnis bleibt in jedem Fall gleich.

Verminderung des Rauschens

Sicherlich werden Sie sich fragen, wo Sie doch von CD-Spielern Werte um 100 dB gewohnt sind, ob bzw. wie man das Rauschen vermindern und damit den Dynamikbereich erhöhen kann. Immerhin liegt der theoretische Wert der Signalquelle um 11,1 dB höher als der Wert, der mit der Schaltung erzielt wurde. Man kann es auch andersherum ausdrücken und sagen, daß das Rauschen der Verstärkerschaltung 11,1 dB beträgt. Ohne Einfluß auf die Signalquelle zu nehmen, bleiben nur drei Möglichkeiten, um Einfluß auf das Rauschen zu nehmen:

1. Verkleinerung der Widerstände, um das thermische Rauschen zu verringern
2. Verringerung des OP-Rauschens
3. Verringerung der Temperatur

Verkleinerung der Widerstände

Wenn man sich die obigen einzelnen Rauschbeiträge im Detail anschaut, sticht U5, also das thermische Widerstandsrauschen der Operationsverstärkerbeschaltung am Minuseingang, ins Auge, das deutlich größer als das Spannungsrauschen U1 des Operationsverstärkers ist. Es drängt sich daher auf, die Widerstände R2 und R3 kleiner zu dimensionieren, um die thermische Rauschspannung zu senken. Man kann deren Werte problemlos auf beispielsweise 10 kΩ bzw. 1,1 kΩ reduzieren, sodaß sich ein effektiver Widerstand des Rückkopplungsnetzwerkes R2 und R3 von ca. 0,99 kΩ ergibt. Mit diesem Wert vermindert sich das Stromrauschen U3 auf 0,14 μV und das thermische Rauschen U5 auf 0,57 μV. Hier die einzelnen Rauschbeiträge im Detail:

U1	Spannungsrauschen des Opamps	18 nV/	→	2,55 μV
U2	Stromrauschen am Pluseingang	9,9 kΩ bei 0,01 pA/	→	0,014 μV
U3	Stromrauschen am Minuseingang	990 Ω bei 0,01 pA/	→	0,0014 μV
U4	Therm. Widerstandsrauschen am Pluseingang	9,9 kΩ	→	1,81 μV
U5	Therm. Widerstandsrauschen am Minuseingang	990 Ω	→	0,57 μV

Das Gesamtrauschen sinkt damit auf 3,18 μV, was einen Signal-Rauschabstand von 69,9 dB ergibt, d.h. eine Verbesserung von sage und schreibe mehr als 6 dB lediglich durch geschickte Widerstandswahl. Das Rauschen des Verstärkers beträgt durch diese einfache Maßnahme nur noch 4,9 dB, was angesichts der geringen Signalspannung nicht schlecht ist. Man kann das Rauschen weiter verringern, indem man R2 und R3 noch weiter verkleinert. Nachteilig dabei ist, daß man dadurch zunehmend den Ausgang des Opamps belastet, was den max. möglichen Spannungshub am Ausgang verringert.

Der Eingangswiderstand R1 liegt übrigens rauschmäßig parallel zu Rg und kommt daher nicht zum Tragen. Man könnte den Wert zwar verringern, um den Wert der Parallelschaltung zu vermindern, jedoch bildet R1 mit Rg auch einen Spannungsteiler, der die effektive Eingangsspannung reduziert. Den Rauschabstand kann man auf diesem Weg daher nicht erhöhen. Deshalb darf (und sollte) man R1 unbeschadet so hochohmig wählen, wie man es für notwenig hält bzw. der OP durch seine Eingangsströme zuläßt.

Ein anderer Weg, das thermische Rauschen zu verringern, liegt darin, die Temperatur der Widerstände zu verringern. Wenn man sie auf den absoluten Nullpunkt (0 K = -273,16 °C) abkühlt, verschwindet das thermische Rauschen sogar völlig. Damit ergibt sich als Gesamtrauschen ein Wert von 2,55 μV entsprechend 71,9 dB Signal-/Rauschabstand. Und das völlig ohne Neudimensionierung der Widerstände.

Rauscharmer Operationsverstärker

Alternativ zur Widerstandsänderung kann man mit einem rauschärmeren Operationsverstärker versuchen, das Rauschen der Schaltung zu senken. Dies ist leider ein in Bastlerkreisen häufig gegangener Weg, der aber -Sie werden es schon ahnen- oft nicht zum Ziel führt. Das Angebot an rauscharmen Operationsverstärkern, die man als Privatperson im Handel auch wirklich kaufen kann, ist leider stark begrenzt. Gut erhältlich und mit 4 nV/

sehr rauscharm ist der NE5534. Ist er also ideal für obige Schaltung? Gern vergessen wird das Stromrauschen, das in den Datenblättern selten auf Seite 1 in der Übersicht der Schlüsseldaten erscheint, sondern z.B. im Datenblatt von Texas Instruments lediglich als eines der zahlreichen Kenndaten beim NE5534 auf Seite 4 aufgeführt wird. Beim NE5534 beträgt das Stromrauschen immerhin 0,6 pA/

, also um den Faktor 60 mehr als beim TL071. Wenn man sich die einzelnen Rauschbeiträge der originalen Schaltung mit den Werten des NE5534 berechnet, erhält man folgende Werte:

U1	Spannungsrauschen des Opamps	4 nV/	→	0,57 μV
U2	Stromrauschen am Pluseingang	9,9 kΩ bei 0,6 pA/	→	0,84 μV
U3	Stromrauschen am Minuseingang	99 kΩ bei 0,6 pA/	→	8,4 μV
U4	Therm. Widerstandsrauschen am Pluseingang	9,9 kΩ	→	1,81 μV
U5	Therm. Widerstandsrauschen am Minuseingang	99 kΩ	→	5,73 μV

Hiermit ergibt sich als gesamte Rauschspannung ein Wert von stolzen 10,4 μV, d.h. der Schuß ging nach hinten los. Der auf den ersten Blick deutlich rauschärmere NE5534 führt in dieser Schaltung also "wundersamerweise" zu einem erheblich höheren Rauschen als der TL071. Wenn man sich die einzelnen Werte ansieht, wird auch sofort klar, warum das so ist: Das im Vergleich zum TL071 hohe Stromrauschen des Opamps führt im Rückkopplungsnetzwerk R2 und R3 zu einer hohen Rauschspannung, die alle anderen Rauschbeiträge dominiert.

Rauscharmer Operationsverstärker mit Optimierung

Jetzt wollen wir versuchen, diesen Rauschbeitrag zu minimieren, um zu überprüfen, ob man die prinzipiellen Vorteile des NE5534 für diesen Anwendungsfall nutzen kann. Dazu muß man das Rückkopplungsnetzwerk R2 und R3 niederohmiger auslegen. Um keine halben Sachen zu machen und das Potential auszureizen, nutzen wir die Tatsache, daß der NE5534 eine leistungsstarke Ausgangsstufe besitzt und recht niederohmige Lasten treiben kann. Daher reduzieren wir R3 auf 1 kΩ und R2 auf 100 Ω, was den effektiven Widerstand des Rückkopplungsnetzwerks auf nur noch 99 Ω vermindert. Dies führt dazu, daß das Stromrauschen nur noch eine Rauschspannung U3 von 0,008 μV hervorruft, während das thermische Rauschen U5 gleichzeitig auf 0,18 μV zurückgeht. Die Rauschbeiträge im Einzelnen:

U1	Spannungsrauschen des Opamps	4 nV/	→	0,57 μV
U2	Stromrauschen am Pluseingang	9,9 kΩ bei 0,6 pA/	→	0,84 μV
U3	Stromrauschen am Minuseingang	99 Ω bei 0,6 pA/	→	0,008 μV
U4	Therm. Widerstandsrauschen am Pluseingang	9,9 kΩ	→	1,81 μV
U5	Therm. Widerstandsrauschen am Minuseingang	99 Ω	→	0,18 μV

In Summe ergibt sich so eine Rauschspannung von 2,0 μV, also deutlich weniger als mit dem TL071. Bei 10 mV Eingangsspannung erhält man damit einen Signal-/Rauschabstand von 74,0 dB, was einer Verbesserung gegenüber dem TL071 von 4,1 dB entspricht. Der Signal-/Rauschabstand ist nur 0,8 dB geringer als theoretisch möglich, d.h. das Rauschen beträgt mit diesen Maßnahmen nur 0,8 dB, was ein ganz hervorragender Wert ist und der Bezeichnung Low Noise mehr als gerecht wird.

Verringerung der Temperatur

Wie man anhand der Berechnungsformeln erkennen kann, ist das thermische Rauschen der ohmschen Widerstände proportional zur absoluten Temperatur. Man kann also ihr Rauschen auf Null verringern, indem man sämtliche Widerstände incl. des Signalquellenwiderstands auf 0 K(-273,16 °C) abkühlt. Dies ist physikalisch leicht erklärbar: Die freien Elektronen z.B. in einem Metallgitter bewegen sich nur dann, wenn man sie mit Energie versieht. Diese Energie wird über die anliegende Temperatur zugeführt. Bei 0 K fehlt diese Energie, wodurch den Elektronen salopp gesagt auch die Energie zum Rauschen fehlt. Eine Temperaturabhängigkeit des Rauschens ist auch bei Opamps gegeben, wird in den Datenblättern aber normalerweise nicht dokumentiert. Da das Spannungs- und Stromrauschen eines Opamps nicht nur durch thermische Effekte sondern zum großen Teil durch die fließenden Ströme verursacht wird, verschwindet das Opamp-Rauschen auch bei 0 K nicht.

In der Praxis ist es allerdings illusorisch, das Rauschen durch Kühlung verringern zu wollen. Den absoluten Nullpunkt kann man ohnehin nicht ganz erreichen. Bereits der Aufwand, eine Abkühlung auf beispielsweise 4 K(-269 °C) vorzunehmen, was man mit flüssigem Helium bewerkstelligen kann, ist beträchtlich und zudem teuer. Wichtig wäre es, vor allem die Signalquelle zu kühlen, da sie oft das limitierende Element darstellt. Wenn die Signalquelle beispielsweise ein Mikrofon, ein Tonabnehmer, ein Tonkopf o.ä. ist, kann man sich leicht vorstellen, daß dies nur ganz selten praktikabel ist. Da man zudem das OP-Rauschen damit nicht allzusehr reduzieren kann, verzichtet man bis auf ganz wenige Ausnahmen (z.B. Forschung) darauf. Zudem benötigt man ganz spezielle Bauteile, weil selbst die teuren MIL-Bauteile (für militärischen Einsatz) nur bis -55 °C spezifiziert sind.

Wer jetzt glaubt, mit Peltierelementen, Trockeneis o.ä. den Durchbruch des Jahrhunderts zu schaffen, sollte sich überlegen, welchen Einfluß die relativ geringe Kühlung überhaupt hat (ganz abgesehen davon, wie praktikabel solche Lösungen wären): Ein Peltierelement schafft im Idealfall maximal 60 K Temperaturdifferenz zwischen heißer und kalter Seite. Wenn man jetzt idealistisch annimmt, daß man die heiße Seite mittels eines extrem großen Kühlkörpers auf Raumtemperatur kühlen kann, ergäbe dies eine Temperatur von 240 K statt 300 K. Die Verminderung des Widerstandsrauschens wäre damit äußerst gering.

Weitere Verbesserungsmöglichkeiten

Man kann zwar versuchen, durch Einsatz noch rauschärmerer Operationsverstärker oder durch noch weiter optimierte Widerstandswerte das Rauschen der Verstärkerschaltung noch weiter zu vermindern, aber dies ist normalerweise nicht sinnvoll. Ob der Verstärker nun 0,8 dB oder 0,4 dB rauscht, läßt sich nur schwer meßtechnisch erfassen, und hören kann man den Unterschied erst recht nicht. Das limitierende Element ist hier die Signalquelle. Wenn man einen deutlich höheren Signal-/Rauschabstand erreichen möchte, bleibt nur der Weg, die Signalquelle anzupacken und entweder ihren ohmschen Widerstand bei gleicher Ausgangsspannung deutlich zu verringern oder aber ihre Ausgangsspannung bei gleichem Widerstand zu erhöhen. Eine höhere Ausgangsspannung bei geringerem Widerstand wäre natürlich noch besser. In den meisten Fällen ist dies aber nicht möglich, weil man Signalquellen nicht ohne Not hochohmig macht.

Wenn Sie das Rauschen der obigen Schaltung von 0,8 dB aus irgendwelchen Gründen trotzdem noch weiter verringern möchten, stoßen Sie auf Schwierigkeiten, denn noch rauschärmere Operationsverstärker zu finden, ist garnicht so einfach. Es gibt zwar Spezialtypen, die noch etwas weniger rauschen, aber diese sind normalerweise für Hobbybastler sehr schlecht erhältlich und zudem empfindlich teuer. Man bewegt sich halt ziemlich nah am technologischen Limit. Durch Einsatz des Typs LT1124 mit e_r = 2,7 nV/

und i_r = 0,3 pA/

könnte man beispielsweise den Signal-/Rauschabstand auf 74,4 dB erhöhen, d.h. das Rauschen auf 0,4 dB verringern.

Tips für die Opamp-Auswahl

Operationsverstärker werden mit verschiedenen Eingangsstufentechnologien hergestellt. Einerseits gibt es Eingangsstufen mit ganz normalen

Sperrschichttransistoren, die unter allen Technologien die niedrigsten Rauschspannungen bieten. Leider besitzen Sie einen nennenswerten Rauschstrom, der den Einsatz auf relativ niederohmige Signalquellen limiert. An der Technologiegrenze kann der Hersteller die Rauschspannung zwar durch Erhöhen des Stroms durch den

Differenzverstärker etwas reduzieren, aber gleichzeitig steigt dabei der Rauschstrom. Die Ursache liegt darin, daß Bipolartransistoren einen kleinen Basisstrom benötigen, wobei der Rauschstrom mit dem Basisstrom korreliert. Erhöht man den Strom durch den Differenzverstärker, erhöht sich bei gleichbleibender Stromverstärkung auch der Basisstrom und damit der Rauschstrom. Solche Operationsverstärker sind dann kompromißlos nur für sehr niederohmige Signalquellen und Gegenkopplungsnetzwerke ausgelegt. Generell sollte man bei Bipolartypen zwar das Gegenkopplungsnetzwerk möglichst niederohmig auslegen, aber andererseits muß man aufpassen, dadurch nicht den Ausgang bzgl. seines Stromliefervermögens zu überfordern. Hier gilt es, einen praktikablen Kompromiß zu finden.

Die Verwendung von

Feldeffekttransistoren in der Eingangsstufe ist in Bezug auf den Rauschstrom sehr vorteilhaft. Auch bei diesem Transistortyp ist der Rauschstrom mit dem Eingangsstrom (hier Gate-Strom) korreliert. Da aber nur ein sehr geringer Gate-Strom fließt, ist automatisch auch der Rauschstrom deutlich geringer als bei einem bipolaren Differenzverstärker. Leider ist das Spannungsrauschen von JFETs etwas höher als bei den bipolaren Typen. Daher eignen sich Opamps mit JFET-Eingangsstufe vorzugsweise für Signalquellen mit mittlerem Widerstand.

Bei sehr hohem Widerstand der Signalquelle (z.B. hochohmige Sensoren) bewirkt selbst der niedrige Rauschstrom von JFET-Opamps eine nennenswerte Rauschspannung. Hier können Opamps mit MOSFET-Eingängen ihre Vorteile ausspielen, deren Rauschstrom bei etwas höherer Rauschspannung um zwei Größenordnungen geringer als bei JFET-Opamps ist. Die Rauschspannung steigt bei allen Opamp-Technologien zu niedrigeren Frequenzen hin an, aber dieser Anstieg beginnt bei MOSFET-Eingängen schon bei recht hohen Frequenzen in der Größenordnung von 1 kHz oder noch höher. Dies ist der sauere Apfel, in den man beißen muß, wenn man auf geringste Rauschströme angewiesen ist.

Generell kann man folgende, ganz grobe Faustregel für die Auswahl der geeigneten Technologie aufstellen, wenn man Wert auf geringstmögliches Rauschen legt:
• Niedriger/mittlerer Signalquellenwiderstand → Bipolar-Eingansstufe
• Mittlerer/hoher Signalquellenwiderstand → JFET-Eingangsstufe
• Hoher/sehr hoher Signalquellenwiderstand → MOSFET-Eingangsstufe

Dies ist wie gesagt nur eine allgemeine Faustregel, wobei es mitunter große Überlappungsbereiche gibt. So kann so mancher rauscharme bipolare Typ auch bei höheren Signalquellenwiderständen oft mit einem Feld-Wald-und-Wiesen-Typ mit FET-Eingängen locker mithalten, speziell wenn es sich bei letzterem um ein Exemplar mit geringem Ruhestrom handelt. Deshalb ist man gut beraten, zuerst einmal das Rauschen einer Schaltung mit einem OpAmp zu berechnen, den man gemäß dieser Faustregel ausgewählt hat. Wenn man wie weiter oben im Berechnungsbeispiel sich die einzelnen Rauschbeiträge ausrechnet, sieht man sofort, wo ggf. der Schuh drückt, und kann sich gezielt auf die Suche nach einem besser passenden OpAmp machen.

Last but not least finden Sie nachfolgend eine Auswahl an rauscharmen Operationsverstärkern, die entweder auch für Elektronikbastler einigermaßen gut erhältlich sind oder die man wenigstens dem Namen nach kennen sollte, weil sie im Zusammenhang mit rauscharmen Verstärkern häufig genannt werden:

Typ	e_r*	i_r*	Ruhestrom**	Technologie	Anz. OpAmps
LT1028	0,85 nV/	1,0 pA/	7,4 mA	bipolar	1
AD797	0,90 nV/	2,0 pA/	8,2 mA	bipolar	1
LT1115	0,90 nV/	1,2 pA/	8,5 mA	bipolar	1
SSM2017	0,95 nV/	2,0 pA/	10,6 mA	bipolar	1
MAX410/412/414	1,8 nV/	1,2 pA/	2,5 mA	bipolar	1/2/4
LT1124	2,7 nV/	0,3 pA/	2,3 mA	bipolar	2
NE5534A	3,5 nV/	0,4 pA/	4 mA	bipolar	1
NE5533A	3,5 nV/	0,4 pA/	4 mA	bipolar	2
NE5534	4,0 nV/	0,6 pA/	4 mA	bipolar	1
NE5533	4,0 nV/	0,6 pA/	4 mA	bipolar	2
LT1113	4,5 nV/	0,01 pA/	5,3 mA	FET	2
NE5532	5,0 nV/	0,7 pA/	4 mA	bipolar	2
RC4156	8,0 nV/	0,15 pA/	1,25 mA	bipolar	4
TLC2272/2274	9,0 nV/	0,0006 pA/	1,1 mA	CMOS	2/4
TL071/072/074	18 nV/	0,01 pA/	1,4 mA	FET	1/2/4
TLC271/272/274	25 nV/	n/a	0,7 mA	CMOS	1/2/4

* bei 1 kHz
** pro Operationsverstärker

Legende:		=	Verweis auf eine andere Datei (Ladezeit)			=	Verweis innerhalb der aktuellen Seite (Zugriff ohne Ladezeit)
		=	Es folgt eine eMailadresse			=	Dies ist ein Download

Alle Angaben in Zusammenhang mit dieser Site wurden nach bestem Wissen und Gewissen gemacht. Trotzdem kann hierfür keine Haftung übernommen werden. Schadenersatzansprüche jeglicher Art sind grundsätzlich ausgeschlossen.

Alle Bilder und Texte sind urheberrechtlich geschützt und Eigentum von Chr. Caspari (sofern nicht anders gekennzeichnet). Es gelten die allgemeinen Benutzungsbedingungen.

Mitteilungen über Fehler sind stets willkommen (Kontaktmöglichkeiten siehe Impressum). Ich bitte um Verständnis, daß mir infolge Zeitmangels keine Beantwortung von Fragen und erst recht keine individuelle Beratung möglich ist - auch nicht ausnahmsweise. Für Fragen zu Pflanzenpflege, Foto und Technik stehen Ihnen jedoch verschiedene Foren ("schwarze Bretter") zur Verfügung.

Letztes Update dieser Seite: 01.10.2023 (Untergeordnete Seiten können aktueller sein)